近来,被应用于自然语言处理领域的变压器不仅被应用于文本,而且还被应用于图像,视频等各种数据,表现出优异的性能。但是,文本,图像和视频分别仅具有1D,2D和3D数据的区别,并且可以视为本质上排成一行的非结构化数据。因此,可以应用相同的转换器算法而无需进行重大更改。
现实世界中的数据并不是独立存在的,而是经常通过数据之间的关系而具有结构化形式。 Netflix和YouTube视频,用户的喜好,游戏玩家及其游戏或购买的物品,此外,人类知识本身并不是一个简单的清单,而是更多相互交织的结构化数据。最近,图形数据库作为表达这些数据的一种手段而备受关注。每个数据在图形数据库中表示为一个实体,每个实体通过一个关系连接,并且每个关系都有一个属性。
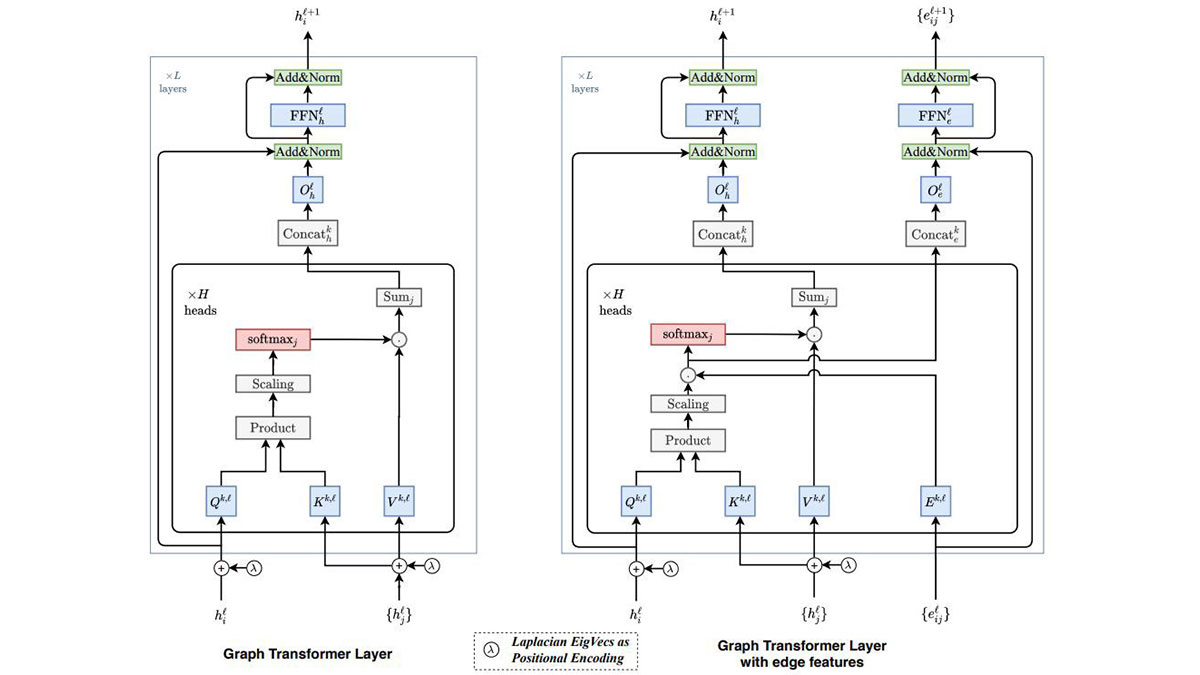
图形转换器是对现有转换器的转换,因此可以将以图形表示的结构化数据用作输入。换句话说,其目的不仅在于学习每个数据的特征,而且在于学习数据之间的关系。为此,进行了两项重大更改。
首先是关注。对于自然语言数据,注意力通常是通过与句子中所有其他单词的连接来实现的。当然,可以通过连接图中的所有节点来实现注意力,但是这种方法效率不高,因为与只有几十个单词的句子中的单词数量相比,图中数据库中的节点数量可能很大。最多。图形转换器通过限制对与相邻节点的连接的关注来缓解此问题。根据应用领域,似乎不仅可以扩展相邻节点(主要邻居),而且还可以扩展相邻节点和重新相邻的节点(次级邻居)。
第二个是位置编码。位置编码用于在给定数据中保留每个实体的唯一位置信息。例如,句子中的每个单词具有不同的位置编码矢量,并且通过反映该位置编码矢量,可以改变句子中单词的出现顺序时具有不同的含义。但是,与自然语言的句子(一维数组)不同,图的节点以更为复杂的方式连接,因此应使用更通用的方法。在图变换器中,拉普拉斯矩阵是表示图中每个节点连接类型的相邻矩阵的扩展,被分解为多个特征向量,所有节点都选择了一些特征向量并将它们用作特征向量。位置编码向量。当将此Laplacian位置编码应用于线性连接图时,它变得与现有转换器中使用的正弦位置编码相同,因此作者说,此方法是现有方法的扩展。
如果已经研究的AI技术主要针对文本,图像,视频和语音等媒体数据,那么我预计将来会出现越来越多针对结构化数据的AI技术。分享与图变压器有关的文章。